數學金字塔
- 向量、矩陣、微積分
- 分析(函數) / 代數(一元二次方程式)
- 幾何(三角形與圓形)
- 座標與圖形、二次函數、圖形關係與證明
- 數學式、集合與機率、平面圖形與立體圖形的性質
將事物用數學來表現,將數字用字母符號代替
四則運算
- 交換律:a+b=b+a
- 結合律:(a+b)+c=a+(b+c)
- 分配律:a(b+c)=ab+ac
- 減法是加上負數:a−b=a+(−b)
- 除法是乘上倒數:a÷b=a×b1
小提醒:分配律常用於展開與因式分解。
機率與集合
- 文氏圖(Venn Diagram)用來表示集合關係。
- 得摩根定律:(A∪B)c=Ac∩Bc,(A∩B)c=Ac∪Bc
- 命題的邏輯推理:如「若 A 則 B」等。
- 邏輯沒有模糊空間,但機率有。
- 機率:事件發生的可能性,P(A)=所有可能結果數有利結果數
- 條件機率:P(A∣B)=P(B)P(A∩B)
- 貝氏定理:P(A∣B)=P(B)P(B∣A)P(A)
例子:
擲一顆骰子,出現偶數的機率?
P(偶數)=63=0.5
定義: 一個輸入對應一個輸出。
一般函數表示:
y=f(x)
一元一次方程式(線性函數)
y=ax+b
圖形為直線,a 為斜率,b 為截距。
直線斜率
斜率公式:ΔxΔy
一元二次方程式(拋物��線)
多少次方就會有多少峰谷,例如二次方程式就是 U 字型
y=ax2+bx+c
解釋:
- 配方法:將二次方程式 ax2+bx+c 轉換成 (x+d)2+e 的形式,方便判斷頂點與開口方向。
- 因式分解:將二次方程式拆成兩個一次因式的乘積,如 ax2+bx+c=(x+p)(x+q),可用於求根。
- 公式解:利用求根公式 x=2a−b±b2−4ac 直接計算方程式的解。
圖形為拋物線,a>0 開口向上,a<0 開口向下,有最大或最小值。
三角形
- 畢氏定理:a2+b2=c2
- 內角和 180∘
- 直角三角形的三角函數應用
- 圓周長 C=2πr
- 圓面積 A=πr2
二項式定理與指數運算
二項式展開
(x+y)n=k=0∑n(kn)xn−kyk
指數函數
y=ax
-
am×an=am+n
-
anam=am−n
-
a0=1;a−n=an1
-
(am)n=amn
-
(a×b)n=anbn
-
(ba)n=bnan
對數函數
y=logax⟺x=ay
尤拉數
e:自然對數的底數,e≈2.718
邏輯斯函數
Logistic Function
邏輯斯函數定義:
f(x)=1+e−x1
- 輸入 x 經過邏輯斯函數後,輸出值會介於 0 到 1 之間。
- 常用於描述機率(如二元分類),也是神經網路中的激活函數之一。
- 圖形呈現 S 型曲線,當 x 趨近於正無限大時,f(x) 趨近於 1;當 x 趨近於負無限大時,f(x) 趨近於 0。
- 在統計學、機器學習(如邏輯迴歸)中廣泛應用。
常用於機率、統計、AI。
三角函數
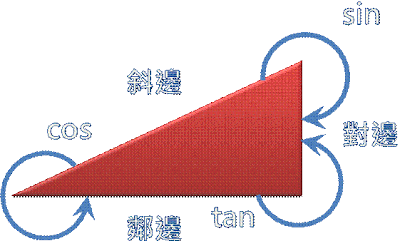
sinθ=斜邊對邊,cosθ=斜邊鄰邊,tanθ=鄰邊對邊
畢氏定理
(計算兩點距離)
c=a2+b2
微積分(Calculus)
微積分是研究「變化」與「累積」的數學領域,包含極限、導數、積分等主題。
詳細內容請見:微積分專章
